MIKU大佬今天出了一道特别有意思的挑战题目，激起了我那浅薄的求知欲。

于是，我尝试用自己还给初中老师的数学知识来分析这道题目，列出几种解题思路，以供大家提高中大奖几率。（伴君一笑）

回归题目本身。

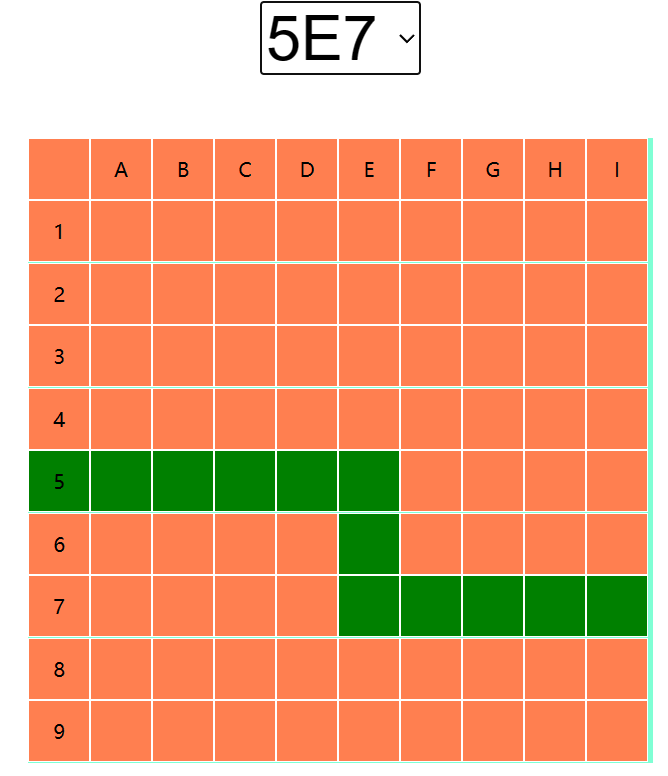
具体规则如下：

有一个横着有9块地板，竖着有9块地板的房间，横坐标轴从a到i，纵坐标轴从1到9，只有一条路线可以通过，你需要根据提示，找到这条路线。

1.只能是从北往南走，或者从西往东走

2.不能走直线，不能走斜线

3.往同一个方向走，最少不能少于2块地板，最多不能多于5块地板

4.转向不能超过2次

5：？？？？？？？？（4月29号晚上八点解锁）

6：？？？？？？？？（4月30号晚上八点解锁）

7：？？？？？？？？（5月1号早上八点解锁）

从已有的4个规则，可以得到以下结论：

1、出发点为1-9和A-I种任意一个，一共有18个。

2、中途必然需要转向2次，所以需要走三步

3、每步只能走2、3、4、5格。

4、第1步和第3步，必然是走4格或5格（由于直线距离需要走满9格）

基于上述分析，路线分歧主要来自于出发点的不同和第2步转向的选择。

而第2步的转向，理论上有8种选择，即上下（或者左右）方向各走2、3、4、5格，但由于受到出发点和格子限制，实际上的选择不会有这么多。

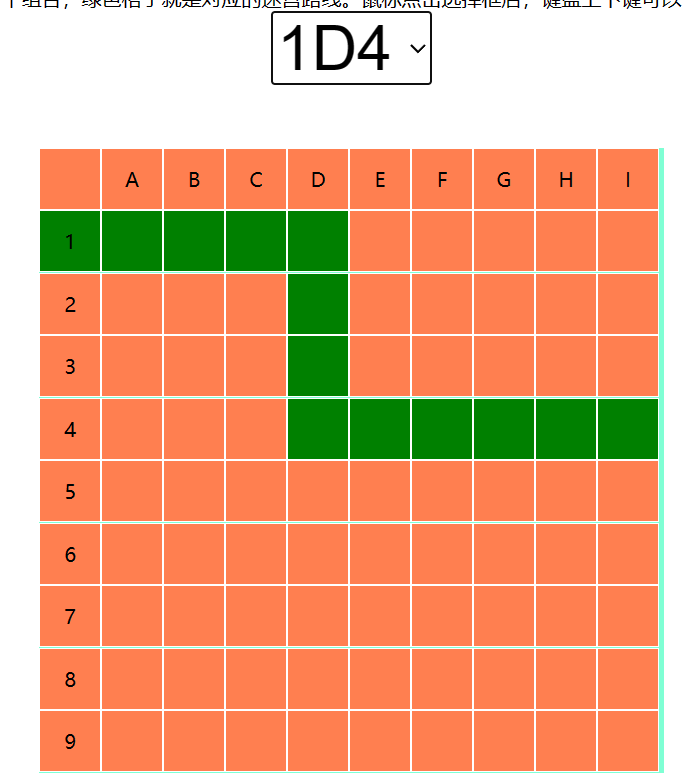
比如，出发点是1的情况（假设第一步走4格），它的中途转向点只有1D3、1D4、1D5、1D6 共四种。而出发点是3的情况，它的中途转向点就有3D1、3D5、3D6、3D7、3D8共五种。出发点是4的情况，它的中途转向点就有4D1、4D2、4D6、4D7、4D8、4D9共六种。

以此类推：出发点为1、2、8、9的选择最少，共4种

出发点3、7选择多一种，共5种。

出发点4、5、6选择最多，共6种。

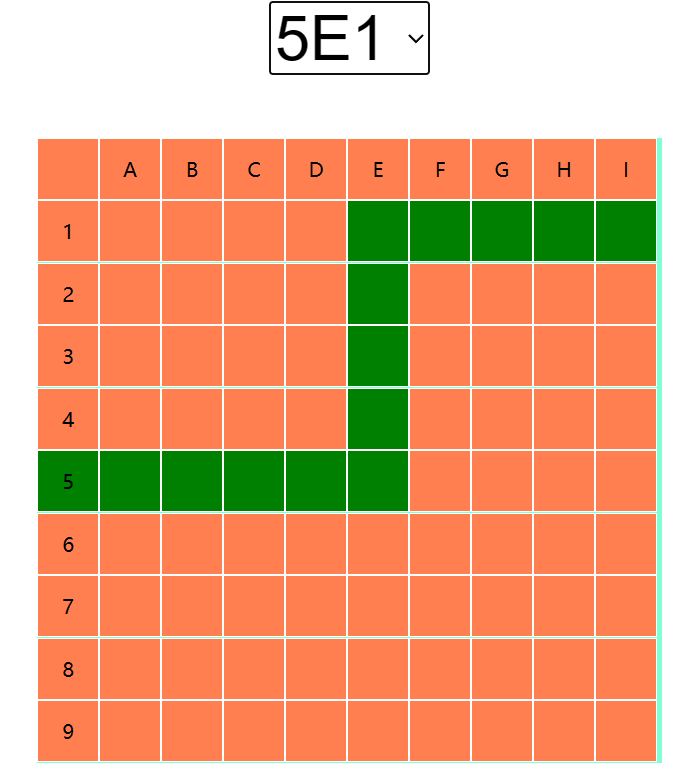
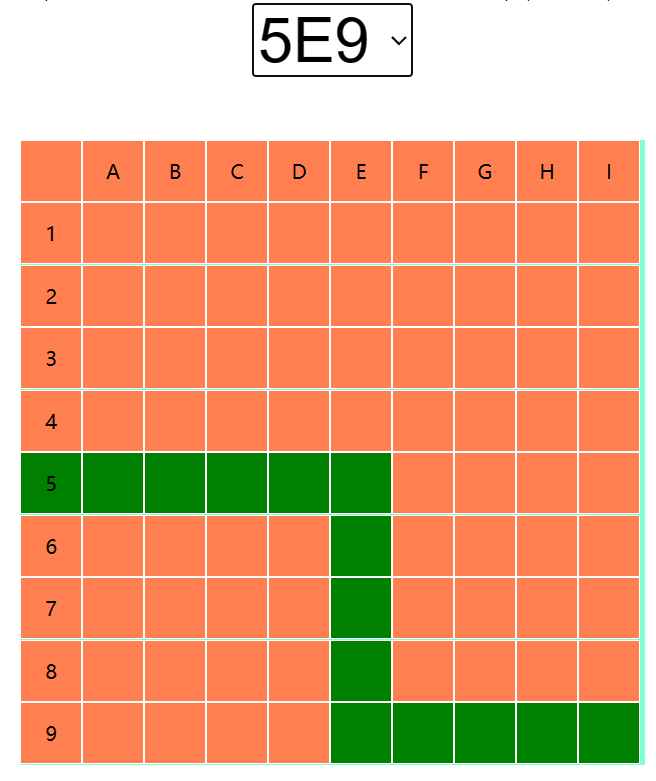
而从字母A—I为对称关系，和1-9数量是一样的。

那么，我们就可以计算出到底有多少种不同路线：18个出发点（x18）*第一步走4格或者5格（x2）*不限制条件下中途转向点的选择（x8）- 不符合条件的线路

不符合条件的线路，可以用上面我们总结出的正确线路规律反推得到，数量为：（8-4）*4（出发点为1289的情况）*2（第一步走4格或者5格）*2（1-9与字母A-I的对称关系）+（8-5）*2（出发点为37的情况）*2*2+（8-6）*3（出发点为456的情况）*2*2=64+24+24=112种

最终得到的可能线路数量为=18*2*8-112=176种

因此，在没有其他因素干扰下，每个人中大奖几率约为1/176。

看起来，似乎并没有那么遥不可及嘛，但鉴于还有很多类似吉影大叔这种5E6上来直接扑街的选手，实际中奖几率还是要高的多，啊哈哈~重在参与嘛。

虽然，MIKU大佬说了还三条线索未公开，但根据帖子有接近100个参与人数来看，现在出大奖概率都超过50%了。

所以建议，想博大奖的同学，今晚八点一定要准时锁定第五条线索，从概率学上来说，只要能将出发点的概率缩减一半（字母OR奇偶性），基本就可以确定大奖得主了。